This blog is the second in a series about agile and risk management. (See the introductory blog, “Three Key Agile Risk Management Activities”). In this blog I introduce a mental model of uncertain events that I will use in the subsequent blogs.
Agile Risk Management & Uncertain Events
There are a number of terms that people use when discussing uncertainty: risk, randomness, volatility, variability, disorder, and so on. I will not address the nuances that distinguish these terms. Instead I will treat them all as synonyms for the same concept that I will refer to as uncertainty.
From an agile product-development perspective, we are interested in uncertain events and the impact that they can have on our ability to produce desirable results. Examples of uncertain events include:
- Earthquake disables California data center housing the development servers
- Vendor fails to deliver a component when promised
- Application fails to scale to 10 million current users
- Requirements change
- The wrong product is built
- Knowledgeable people leave the company
At this point you are probably thinking about the many other types of uncertain events you have dealt with on your own projects.
Mental Model of Uncertain Events
The image below illustrates a mental model of uncertain events.
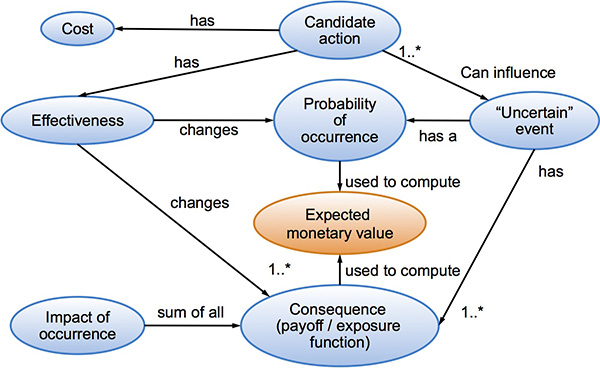
Starting on the right side, we have uncertain events that might happen. For example, Sarah, the only person who knows a critical area of the code, might leave the company.
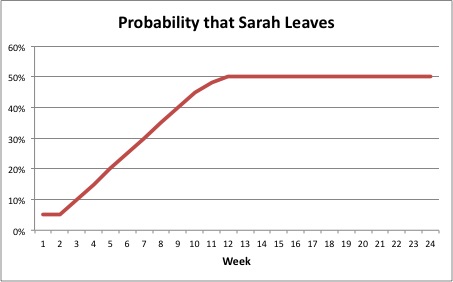
Each uncertain event has a probability of occurrence (how likely is it the event might happen). We might ask ourselves: “How likely is it that Sarah might leave the company?” There may be a single number answer to that question—“We believe there is a 50% probability that Sarah might leave.” Alternatively, if the likelihood of an uncertain event depends on a variable whose value can vary over a range (such as time), we could describe the likelihood of the event as a discrete or continuous probability distribution.
For example, we might ask the question about Sarah leaving at different points in time: “What is the probability that Sarah will leave next week?” We might estimate that probability at 5%, where as the probability that she might leave within three months might be 50%.
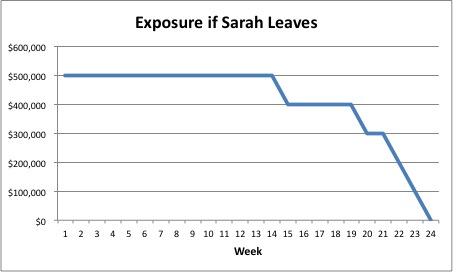
Every uncertain event is associated with one or more consequences. For example, if Sara left, one consequence could be a substantial delay in our next product release. We could calculate the consequence of her departure by determining the cost of delay of not having the product available for sale when originally expected. Like the probability of occurrence, the consequences might be expressed as a single number, a series of numbers, or a continuous function, described as a payoff or exposure function.
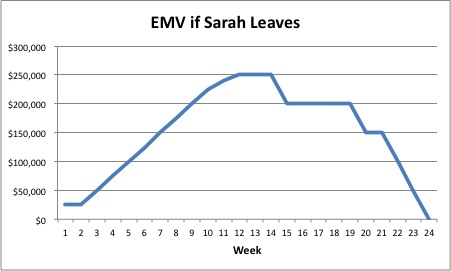
The expected monetary value (EMV) is calculated by multiplying the probability by the consequences. So if there were a 50% probability that Sarah might leave, and the consequence of her leaving would generate a $500k cost of delay in the next release of our product, then the EMV is $250k (50% * $500k). Again the expected monetary value might be described over a range of values calculated by multiplying the probability distribution function by the payoff or exposure function.
Risk Mitigation & the Mental Model of Uncertain Events
Identifying and quantifying risks are important, but so is risk mitigation. Shown on the top part of the mental model is the concept of candidate actions that we can take, at a cost, which might change the probability of occurrence or consequences (for better or for worse).
For example, one candidate action we might take with Sarah is to slap a pair of golden handcuffs on her (basically we offer her a lot of stock options to make it financially very painful for her to leave the company). This action has a cost—we have to grant her the stock options—that has financial ramifications to the company.
Our hope is that this action will reduce the likelihood that Sarah will leave the company. Perhaps now we think there is only a 1% probability that she will leave the company within six months. That’s good, since when we recalculate our expected monetary value, our action changes the EMV from $250k to $5k (1% * $500k).
Note that in this circumstance, the action of giving her lots of stock options would change the probability of her leaving, but it does not affect the consequences if she does. Meaning if she leaves, regardless of whether or not we granted her the stock options, we still would experience the same $500k cost of delay.
Of course, for a cost we could also take actions to mitigate the consequences. For example, we could start training other people in the area of code that only Sarah knows. This action, however, does not change the probability that Sarah will leave. (If it did, it might actually increase the probability of Sarah leaving!) Frequently a given action will affect only the consequences or the probability, but not both. We should seriously consider taking any low-cost action that simultaneously improves the probability and the consequences of an important uncertain event.
Summary
This model of uncertain events is not only intuitive, but it is also quite powerful. I will leverage it in future blog posts to better elaborate how we deal with uncertainty (risk) when applying agile development. The next blog in this series introduces the concept of antifragility & how it applies to dealing with risks during agile development.